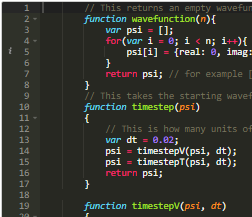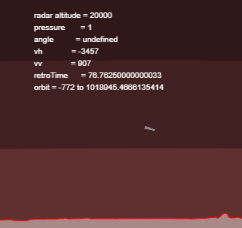
The wavefunction shown in the previous picture has to be antisymmetric: When you reverse any two inputs, you get the negative of the output.
A common way to generate an antisymmetric function is to write it like this:
$$\psi(\mathbf{x}) = J(\mathbf{x}) \det{\begin{bmatrix} f_1(x_1) & f_1(x_2) & ... \\ f_2(x_1) & f_2(x_2) & ...\\...&...&... \end{bmatrix}},$$
where $\mathbf{x}$ is the vector of positions, and $x_1$ is the first of those, etc. $J(\mathbf{x})$ has to be symmetric, which is easy to generate. $J$ is called the Jastrow function.
For instance, any function of just the distances between the particles, or the distances between particles and nuclei, will by symmetric (swap any two inputs and get the same answer).
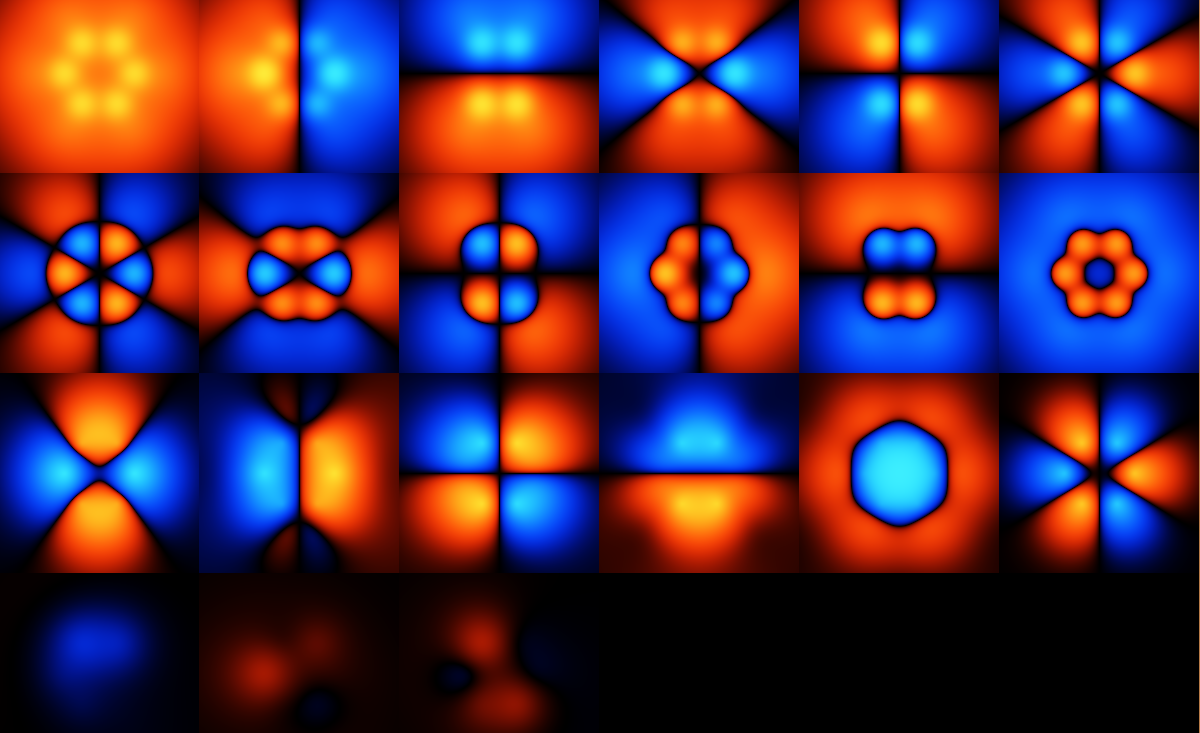
In the image above, the various functions $f_i(x)$ are plotted. Note that these are my choice of function, and not the *real* ones, given that the real system doesn't exactly
obey any equation like the one above. However, these functions are a fairly natural basis set for things like benzene, although it may be that the electrons end up too delocalised when using this --- I don't have the experience to know unfortunately.
The basis set here doesn't have to be orthogonal, and it's not.
The basis set above might seem somewhat arbitrary, and again might raise the question of how we know the answer is right,
if we can keep making up functions arbitrarily. The main answer is again that if we get the guesses wrong, the energy result will
be strictly too high: The lower the output energy is, the closer the wavefunction must be to being correct. The basis set above is locally optimised to get as low energy as possible,
which is the sense in which these are not arbitrary.
A second answer is that there is a trick to improve upon the guessed wavefunction using a diffusion process, which again insulates us from having
guessed an inaccurate wavefunction.
 The wavefunction shown in the previous picture has to be antisymmetric: When you reverse any two inputs, you get the negative of the output.
A common way to generate an antisymmetric function is to write it like this:
$$\psi(\mathbf{x}) = J(\mathbf{x}) \det{\begin{bmatrix} f_1(x_1) & f_1(x_2) & ... \\ f_2(x_1) & f_2(x_2) & ...\\...&...&... \end{bmatrix}},$$
where $\mathbf{x}$ is the vector of positions, and $x_1$ is the first of those, etc. $J(\mathbf{x})$ has to be symmetric, which is easy to generate. $J$ is called the Jastrow function.
For instance, any function of just the distances between the particles, or the distances between particles and nuclei, will by symmetric (swap any two inputs and get the same answer).
In the image above, the various functions $f_i(x)$ are plotted. Note that these are my choice of function, and not the *real* ones, given that the real system doesn't exactly
obey any equation like the one above. However, these functions are a fairly natural basis set for things like benzene, although it may be that the electrons end up too delocalised when using this --- I don't have the experience to know unfortunately.
The basis set here doesn't have to be orthogonal, and it's not.
The basis set above might seem somewhat arbitrary, and again might raise the question of how we know the answer is right,
if we can keep making up functions arbitrarily. The main answer is again that if we get the guesses wrong, the energy result will
be strictly too high: The lower the output energy is, the closer the wavefunction must be to being correct. The basis set above is locally optimised to get as low energy as possible,
which is the sense in which these are not arbitrary.
A second answer is that there is a trick to improve upon the guessed wavefunction using a diffusion process, which again insulates us from having
guessed an inaccurate wavefunction.
The wavefunction shown in the previous picture has to be antisymmetric: When you reverse any two inputs, you get the negative of the output.
A common way to generate an antisymmetric function is to write it like this:
$$\psi(\mathbf{x}) = J(\mathbf{x}) \det{\begin{bmatrix} f_1(x_1) & f_1(x_2) & ... \\ f_2(x_1) & f_2(x_2) & ...\\...&...&... \end{bmatrix}},$$
where $\mathbf{x}$ is the vector of positions, and $x_1$ is the first of those, etc. $J(\mathbf{x})$ has to be symmetric, which is easy to generate. $J$ is called the Jastrow function.
For instance, any function of just the distances between the particles, or the distances between particles and nuclei, will by symmetric (swap any two inputs and get the same answer).
In the image above, the various functions $f_i(x)$ are plotted. Note that these are my choice of function, and not the *real* ones, given that the real system doesn't exactly
obey any equation like the one above. However, these functions are a fairly natural basis set for things like benzene, although it may be that the electrons end up too delocalised when using this --- I don't have the experience to know unfortunately.
The basis set here doesn't have to be orthogonal, and it's not.
The basis set above might seem somewhat arbitrary, and again might raise the question of how we know the answer is right,
if we can keep making up functions arbitrarily. The main answer is again that if we get the guesses wrong, the energy result will
be strictly too high: The lower the output energy is, the closer the wavefunction must be to being correct. The basis set above is locally optimised to get as low energy as possible,
which is the sense in which these are not arbitrary.
A second answer is that there is a trick to improve upon the guessed wavefunction using a diffusion process, which again insulates us from having
guessed an inaccurate wavefunction.