Quantum Monte Carlo Gallery
I tried, over a month or two, to get ground states for some simple molecules: H, H2, H2O, C, C2, C6H6-benzene.In terms of energy, The binding energy of water and C2 is about 70 Hartrees, where a Hartree is about twice the ionization energy of Hydrogen.
I managed to get to about 1 Hartree of the right answer, which is good enough to see that the process sort-of works, but not close enough to answer questions like "what is the minimum energy bond angle of water".
Instead of writing it up properly, which would take ages and not be all that interesting, I thought I'd produce a captioned image gallery instead.
The thing you're trying to model, when trying to get accurate energies for benzene, is its wavefunction. The wavefunction is a function that takes as input the 3D positions of the 42 electrons, and outputs one number.
As a kotlin function, for instance, its type is:
fun psi(x : Array<V3>, spins : Array<Boolean>) : Double
In general, the output can be complex, but I'm fairly sure that in the absence of a magnetic field, the minimum energy
wavefunction can always be written as a purely real function, and therefore the return type can be just Double.
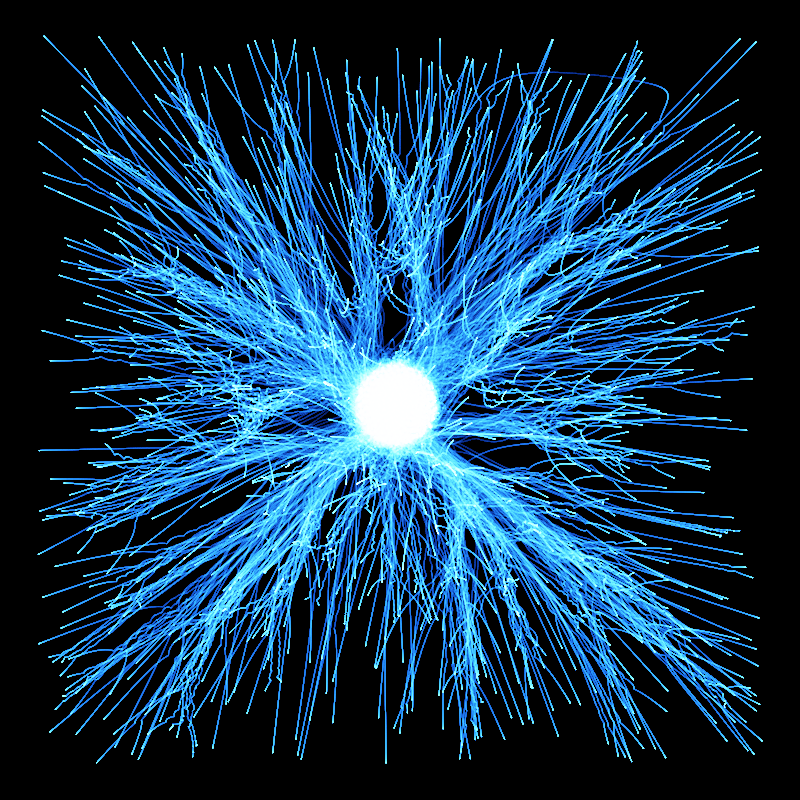
The image above is what happens if you plot a cross section through the wavefunction - varying the point you take a cross section through.
The wavefunction shown above is accurate enough to get the energy to about 1 or 2 % of the total binding energy.
In many ways to get chemical energies, the game is to pick a wavefunction, then calculate the energy for that wavefunction, and then keep trying variations of the wavefunction to try to minimise the energy.
When you're trying to work out the energy, if there's no bug in your code, and provided the wavefunction you've chosen's local energy is well behaved, and provided that the wavefunction is antisymmetric (if you swap any two inputs, you get a negated output) you cannot accidentally get too low an energy.
This means that you can add as many parameters as you want to your wavefunction, without worrying that you could get the right energy, but be completely wrong about the wavefunction.
Next Page
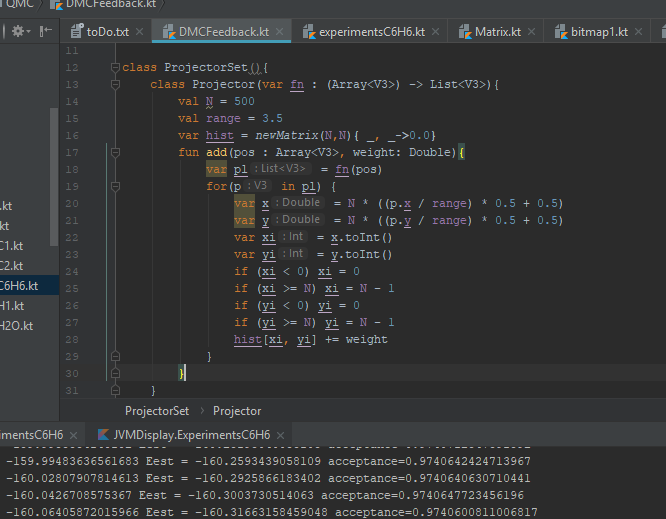I chose to use Kotlin for this project because it's concise, easy to use, good it's got a good IDE with IntelliJ and it's reasonably fast.
I think Kotlin is a language improvement over C#, which is an improvement over Java. In both cases, the improvement is better functional style stuff, and more concise. It feels like a silly point, but I like being able to have multiple main functions in a file in Kotlin, which I believe is not possible in C#.
C#, though, has (in my opinion), a slightly better IDE, with visual studio, and better interop at the moment with native code. It is easier to do memory management in C# than kotlin as far as I can tell, although I haven't done
performance benchmarks to see if that actually changes the performance noticeably.
Regarding C++, I assume that it would be faster than Kotlin, and I would sacrifice a bit of language points for performance points. I might try a project in C++ next for that reason.
I wonder, a bit, whether the GPU would be the key to performance, though, and it may be that kotlin's GPU access is good enough to get this performance anyway without using C++.
Briefly: one language thing I don't like in Kotlin is the requirement to have ".toDouble()" when converting from int to double. Kotlin seems to use "if (condition) a else b" instead of "condition?a:b", and I prefer the "?" way. But these aren't big problems, and overall, I do really like Kotlin.
Next Page
Other Articles:
|
How to simulate fractal ice crystal growth in PythonThis presents python code to draw snowflakes, simulating a diffusion process with Fourier transforms. |
Mars Re-EntryA ThreeJS simulation of Mars re-entry in a spaceship. |
|