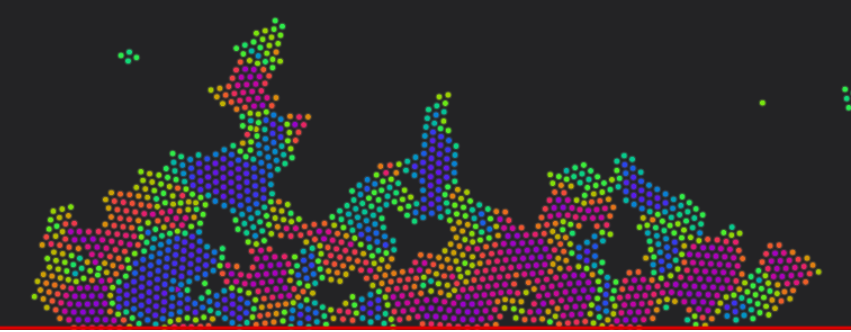
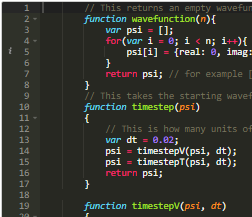
We guessed (with some optimisation) a wavefunction for Benzene that was somewhat realistic. Diffusion Monte Carlo allows you
to improve upon your energy estimate using the following observation.
Let's define a new function, $f$ like this:
$$f(\mathbf{x}) = \psi_{true} \psi_{guessed}.$$
This new function $f$, has two important things about it:
- The weighted average local energy, weighted by f, taking the local energy to be the energy of the guessed wavefunction, is actually the true energy. (Subject to the guessed wavefunction having correctly placed nodes).
- We can actually generate a series of points with a population density proportional to $f(\mathbf{x})$, even though we don't know what $\psi_{real}$ is.
This is very helpful: We don't know what the real wavefunction is, but can generate a population of points that follows something related to it. And luckily, that something related to it has a way to get the "true" energy from it.
The way to get a population of points with density $f(\mathbf{x})$ comes from the observation that if we assume that the energy of the wavefunction $\psi_{real}$ is minimal, and we use the normal Schroedinger equation to define the energy,
we can derive that:
$$\frac{\partial f}{\partial t} = \frac{1}{2}\nabla_i f - \nabla . \frac{\nabla \psi_{guess}}{\psi_{guess}} f + (E(\mathbf{x}) - E_{target})f,$$
here $t$ is a variable that as it increases, $f$ tends to the correct value. When interpreted as a diffusion equation, $t$ is time.
This equation is simply a diffusion equation with some forces: It's exactly the same equation you would use to track suspended bacteria particles in moving air. The particles need to be able to divide, and die off too, to get the equation to match, but that isn't hard to simulate.
So all we do is make an educated initial guessed wavefunction, and then run such a simulation, and that gets us a million or more particles whose distribution in space is equal to $f(\mathbf{x})$. And if we average the local energy over the positions of all
these particles, we'll get the true energy.
Or not. Unfortunately, there is a requirement that the positions where the guessed wavefunction is zero, are correct, and that can lead to inaccuracy.
Another problem is that you need to run this for a long time before you get a completely smooth distribution of $f$. The smoothness itself doesn't matter, but it isn't good to have
big regions of space with few or no particles, and that leads to random noise in the energy estimate.
