Maths Exam
| 1. | Solution of linear equations
|
| 2. | Differentiation A
|
| 3. | Differentiation A
|
| 4. | Differentiation B
|
| 5. | Integration
|
| 6. | Integration
|
| 7. | Consider the following differential equation: $$ 5\frac{d^2y}{dx^2} - 4\frac{dy}{dx} - y = 0 $$
|
| 8. | Consider the following series: $$ \sum_{j=0}^{15} -4\left(j + 1\right) $$
|
| 9. | Solution of linear equations
|
| 10. | Differentiation A
|
Other Articles:
|
Physics Algorithms BookThis is a work in progress to write a book on physics algorithms. At the moment, it is about 1/3 finished though, but the latest version can be downloaded for free. |
|
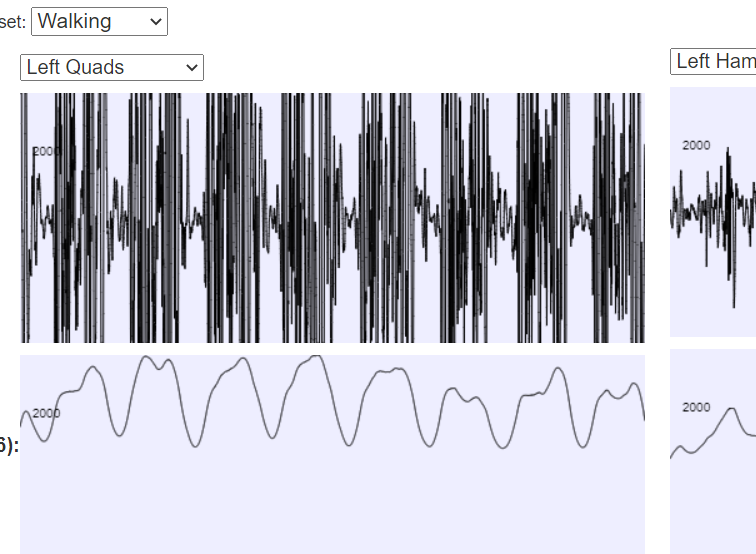
BodyWorks: EMG AnalysisA page with a javascript application where you can interact with EMG data using various filters. |

|
Moon FormationA Kotlin N-Body code, and lots of animations of the collision between Earth and a hypothetical Theia that people think created the moon. |