Quantum Mechanics without the maths or philosophy
Previous Page
Point 5: Potentials
All the examples above begin with "A single electron is floating around in free space".You can add a term to the equation to represent the fact that the electron is attracted to a proton.
 |  |
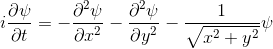- The experimenter puts an electron in a region of space near a proton
- The electron has a very uncertain momentum
- The electron does one of two things. There is a chance that it escapes (resulting in what looks like an initial explosion).
- There is a chance that the electron will be bound to the proton.
- Although bound to the proton, the electron's wavefunction moves around.
Summary
You can easily add something to the Schrödinger equation that makes the electron interact with a proton. When we try this, we get a simulation in which the electron seems to stick around. In previous examples, the electron tended to move freely round its enclosure. Now we've got an electron whose wavefunction stays high at the centre of the box - which is where the nucleus is.
To express that differently, no matter how long you wait, the electron will always have a probability of being near the nucleus. An electron plus a nucleus, when bound like this, equals an atom.
Unnecessary Notes
Skip ahead, if you want, but here are some other thoughts.
Skip ahead, if you want, but here are some other thoughts.
- The initial conditions of this experiment are not very realistic: you don't generally create atoms by putting an electron nearby and then waiting: you normally start with atoms already constructed, or have free electrons emit photons to become bound. This process is much more complicated than the simulation above.
- This simulation has an initial explosion, followed by a short interference pattern. The enclosure here is designed to absorb the electron, but it's not perfect, and so there is a chance that the escaping electron bounces off the enclosure. That creates a brief, slight, interference pattern.
- The atom here is moving around quite a bit - most atoms we meet don't do that for the simple reason that atoms at room temperature tend to be in the ground state. Atoms in the ground state have electron probability functions that don't move. In fact, every state is like that: the movement occurs when the electron is not in a definite energy level.
Point 6: Spectra
In the previous experiment, the electron clearly moves about. The electron is negatively charged. We know that charged particles that accelerate generate electromagnetic radiation.We also know that real atoms also emit electromagnetic radiation when they're excited.
We can use a spectrometer to see what frequencies of radiation are given off by real atoms.
We can simply plot the average movement of the electron in our new quantum theory - shown below:
| |  |
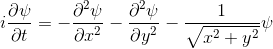If you compare the frequencies coming from real life hydrogen to the frequencies coming from our crude simulation, they match almost perfectly (at least if you do the calculation in 3d).
Summary
We can show experimentally that this simple Schrödinger equation gives accurate predictions of the frequencies of radiation coming off real hydrogen atoms.
This is evidence that not only is the theory vaguely correct in that it is a wave and stuff, it's actually quite accurate.
This is a skippable point, but it is interesting if you wish to know why people believe that quantum mechanics works.
Point 7: Two electrons
We started off with a simple wave equation. Then we added a term to it that is the attraction between the electron and a nucleus. The result let us accurately predict the emission spectrum for atomic hydrogen.Now let's consider a 2-electron example.
In order to show 2 electrons in a 2d animation, we're going to have to constrain each electron to be just in one dimension. You, the reader, have to stare at the following picture until you understand the following:
- There are two electrons.
- Each electron is in a 1-dimensional enclosure.
- Electron 1 is most likely to be at the left.
- Electron 2 is most likely to be in the middle.
(If you're worried about exchange symmetry ... read on.)
So. Here goes: A 2-electron wavefunction: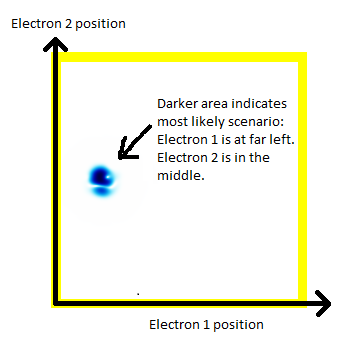
And the corresponding animation:
(a) The story here is that the blob starts off at the left and moves to the right. That should be interpreted as electron 2 is in the middle, electron 1 is below it (for electron 1, up and down become right and left in the diagram only).
(b) The blob doesn't cross a diagonal dividing line running from bottom left to top right. This dividing line is every configuration where the two electrons are at in the same place. So the observation that the blob doesn't cross the dividing line is actually the observation that electron 1 remains below electron 2.
Complete story: Electron 1 is moving upwards. Electron 2 is stationary. Then electron 1 collides with electron 2, sending electron 2 upwards.
Summary:
We can add another electron to make a 2-electron system, quite simply, by adding in another set of coordinates. In these diagrams, we'll use the x axis as electron 1's position, and the y-axis as electron 2's position.
The Schrödinger equation hardly changes.
Make sure you understand the diagram above and the animation, because otherwise not much will make sense later on.
The 3rd (and final) part of this article is on the
So. Here goes: A 2-electron wavefunction:
And the corresponding animation:
 |  |
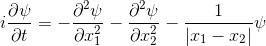(a) The story here is that the blob starts off at the left and moves to the right. That should be interpreted as electron 2 is in the middle, electron 1 is below it (for electron 1, up and down become right and left in the diagram only).
(b) The blob doesn't cross a diagonal dividing line running from bottom left to top right. This dividing line is every configuration where the two electrons are at in the same place. So the observation that the blob doesn't cross the dividing line is actually the observation that electron 1 remains below electron 2.
Complete story: Electron 1 is moving upwards. Electron 2 is stationary. Then electron 1 collides with electron 2, sending electron 2 upwards.
Summary:
We can add another electron to make a 2-electron system, quite simply, by adding in another set of coordinates. In these diagrams, we'll use the x axis as electron 1's position, and the y-axis as electron 2's position.
The Schrödinger equation hardly changes.
Make sure you understand the diagram above and the animation, because otherwise not much will make sense later on.
The 3rd (and final) part of this article is on the
Next Page
Other Articles:
AsciishipMy latest (early 2018) thing is just a "normal" game: no real physics. It's just a game. |
|
|
Quantum Mechanics for programmersA quick demo showing how to make simulations of simple quantum mechanics systems in javascript. |
Simulation of flooding in New OrleansA not-very-accurate simulation of the flooding in New Orleans. |
|
© Hugo2015. Session @sessionNumber