Atomistic Metals
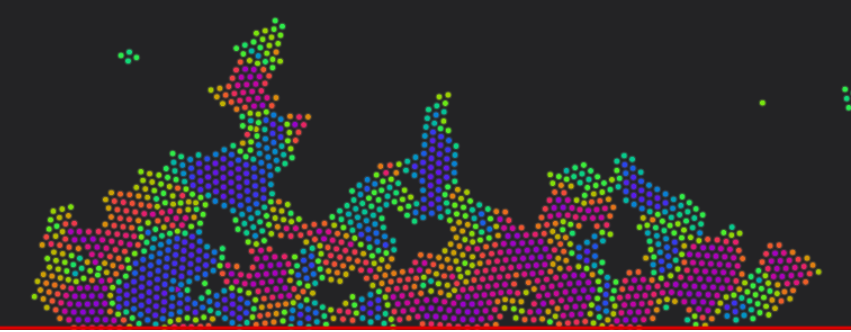
In the interactive simulation below, you choose a procedure to form a piece of metal. It shows how the atoms in a metal arrange to form domains.
Things you can do in the simulation:
- You can drag the red lines around using the mouse.
- You can set the temperature, using the slider below the chart.
- You can measure the strength of the material using the button below the chart. Note that this test has several problem as it stands.
- You can drag the circles around in the top left corner.
- You can choose the material from the dropdown below:
Caveats:
- This is a fictional metal in two dimensions. It's only meant to demonstrate the principles, not the details of real metals.
- The lump formed here is only 3nm across, much smaller than you could see in a microscope even, and on the smallest scales, things can deform differently than larger lumps.
- Time is slowed down dramatically - the barriers move when you drag them, but even a modest speed is probably faster than the speed of sound. This is responsible for the jelly-like behaviour of the material.
- The force measurement is very crude - it may be of interest, but don't draw too many conclusions from it. In real life, having a few big crystals would make a softer metal, but here the opposite is true, possibly because the failure modes of tiny crystals are different to large ones.
What's going on?
We have 1500 atoms that naturally clump together in a similar way to how they clump in metals: Individual molecules don't typically form, but bulk lumps do. They are simulated in a heat bath, keeping the material at a prescribed temperature. At high temperatures, atoms jiggle around a lot more, eventually jiggling so much that the lump melts then vaporises.The colour of each atom depends on its neighbours. If the neighbours are aligned horizontally, the atom is one colour. If it is rotated slightly, it changes to a different colour. The aim of this colour scheme is to show the different grains or domains within the lump: One domain will be a uniform-ish colour, and have a different colour around it. Grain boundaries can be any colour, and atoms around a defect are typically another colour again.
The different materials have different atomic properties, in particular, material 1 has a more localised attraction potential, and grain boundaries, slip surfaces and defects move much less than the other materials. By contrast, in material 3, the grain boundaries and defects move much more readily.
Alloys have two types of atoms, both with very similar atomic properties, but different radii.
No quantum mechanics is simulated here: The only physics here is a pair-wise potential between nearby atoms.
Challenges?
- Try to create a square object with one grain only. It should be a uniform colour apart from the edges.
- Try to create a square object with many grains.
- What is the melting point of the substance?
- What is the boiling point of the substance?
- Is it stronger hot or cold?
- Is it stronger as one grain or many? (Note that this is possibly different in real life / for larger systems).
Other Articles:

|
Saturn's ringsA simulation of Saturn's rings --- a few thousand particles are simulated, in a repeating tiled region. You use the mouse and keys to fly in it. |
AsciishipMy latest (early 2018) thing is just a "normal" game: no real physics. It's just a game. |

|
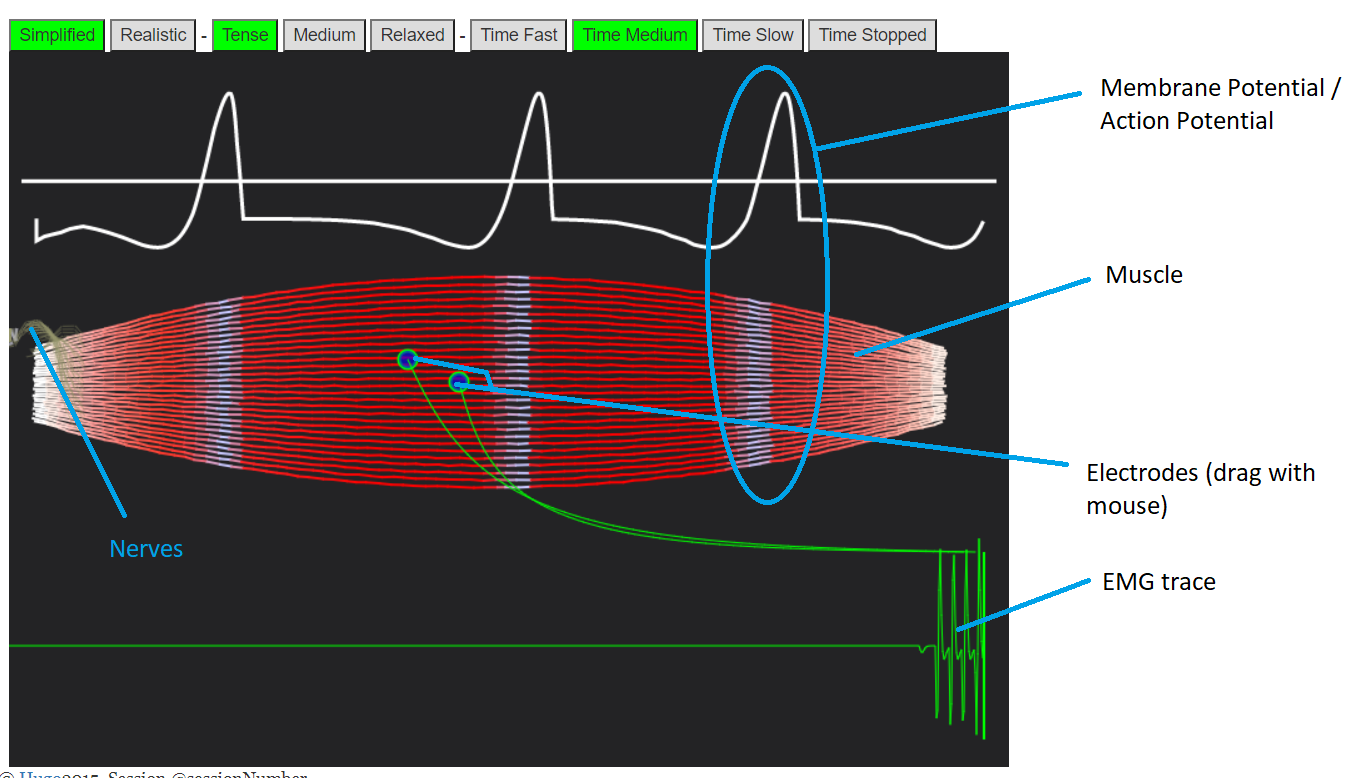
|
BodyWorks: Neuromuscular Activity / Muscle EMGAn interactive simulation showing how nerves travel to and down muscles, and how this gets picked up by EMG sensors. |