Maths Exam
| 1. | Expand the Brackets
|
| 2. | Expand the Brackets
|
| 3. | Collect Like Terms
|
| 4. | Adding fractions
|
| 5. | Evaluate the following equations.
|
| 6. | Rearrange the following equation.
|
| 7. | Quadratic Equation
|
| 8. | Expand the Brackets
|
| 9. | Expand the Brackets
|
| 10. | Collect Like Terms
|
Other Articles:
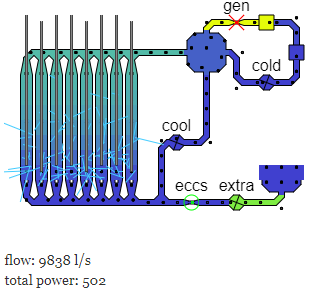
|
Chernobyl SimulationAn attempt to simulate the normal running, and then accident of the Chernobyl nuclear reactor. |
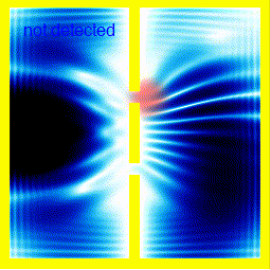
|
The double slit and observersA look at the double slit experiment. The first half is meant to be a clear explanation, using simulations. The second half discusses some of the philosophy / interpretations of quantum mecahnics. |
Benzene QMC GalleryA gallery of images from an attempt to model the benzene ground state using a variational and diffusion monte carlo method. |
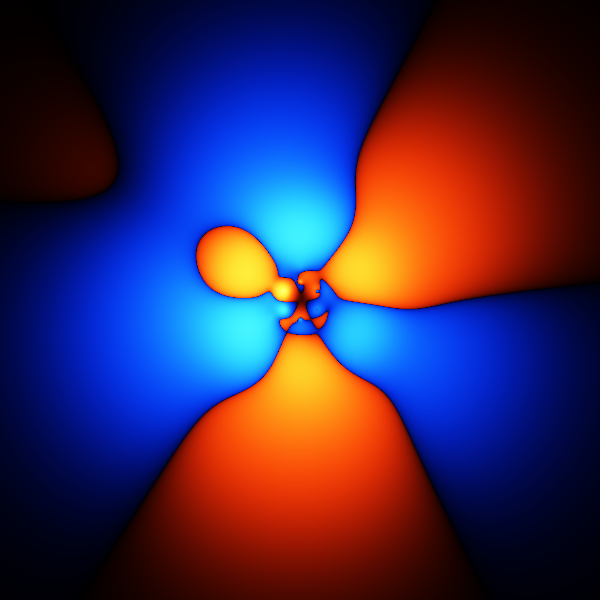
|